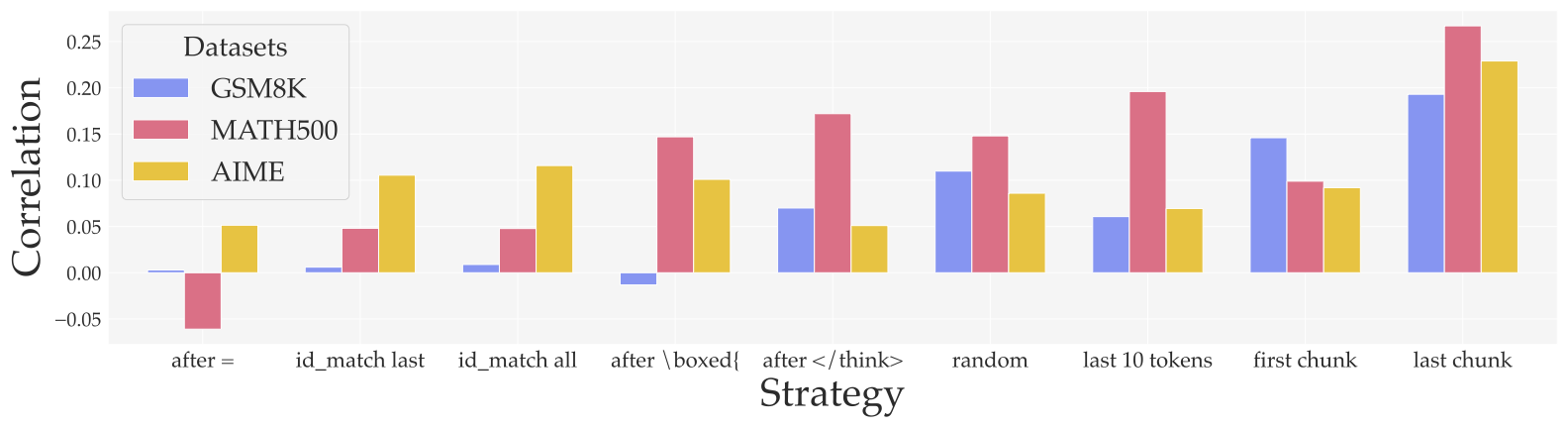
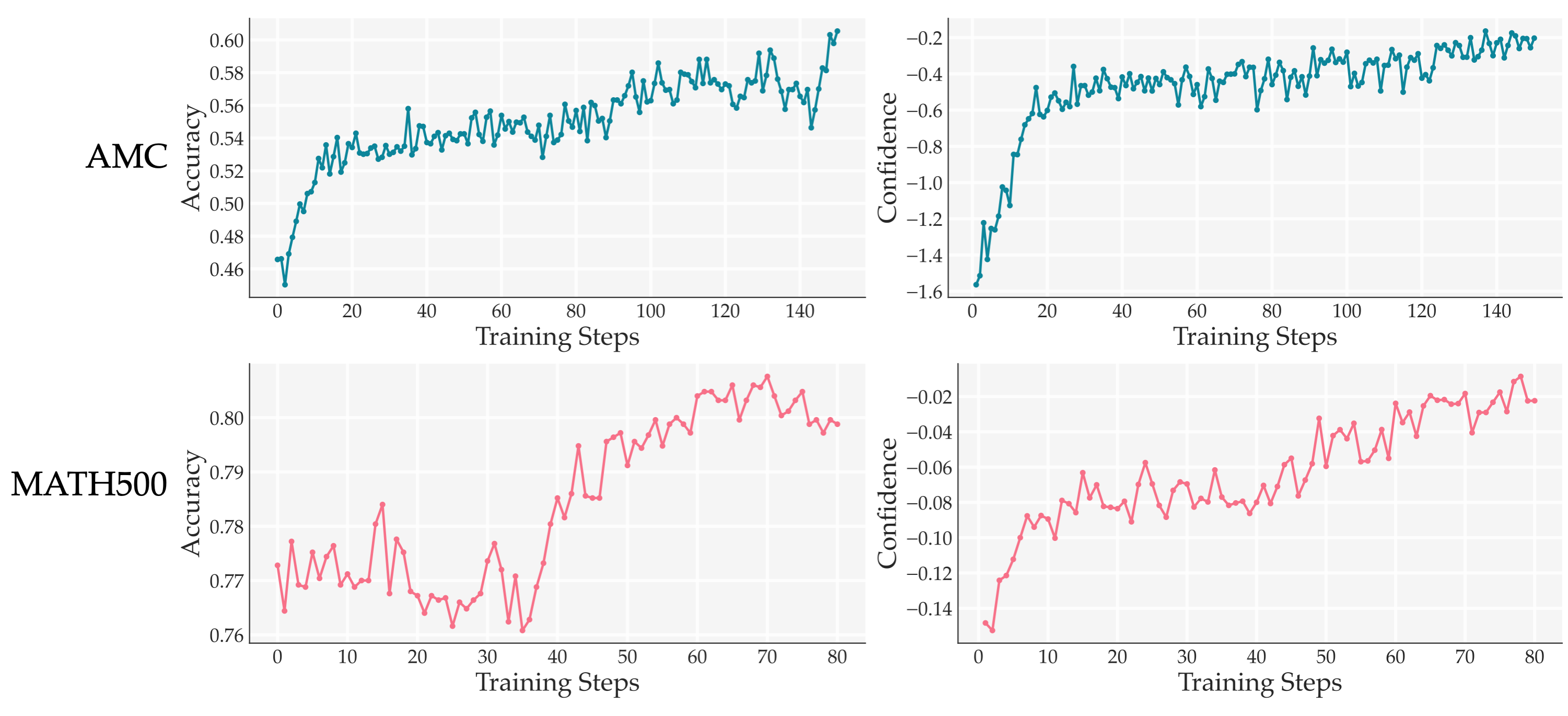
RENT: Reinforcement Learning via Entropy Minimization is a fully unsupervised reinforcement learning method that improves reasoning performance by using the model's own confidence as a reward. Given an input problem \(\mathbf{x}\), the model generates a reasoning chain \(\mathbf{y} = \pi(\mathbf{x})\) and receives a reward based on the negative entropy of its token predictions: \(R(\mathbf{y}) = -H(\pi(\mathbf{x}))\). This encourages the model to produce more confident predictions. We find that minimizing entropy over tokens near the end of the reasoning chain correlates most strongly with improved accuracy. RENT requires no external reward or ground-truth answers and consistently improves performance across diverse reasoning benchmarks including GSM8K, MATH500, AMC, AIME, and GPQA.